Transformers are one of the most popular architectures used in both sequence modeling and computer vision. At the center of Transformers is the attention mechanism, which compares each element of a sequence with every other element. This pairwise similarity score is used to decide how much the other tokens contribute to the new representation of one element. While the approach gives state-of-the-art results, it comes at the cost of quadratic time complexity. Additionally, for language generation, the next token prediction is linear in the prompt length, compared to the constant time complexity of approaches like Structured State Models (SSMs).
We introduce Latte, a new linear time and memory replacement for standard attention, which achieves a comparable performance to Transformers while being more efficient during training and inference. These properties are important for document modeling or high-resolution visual question answering, where input can be very long. In this blog post, we focus on an intuitive explanation of Latte, but the approach is inspired and can be easily understood from the lens of latent variables. For a concise mathematical explanation, check out our paper.
We will first rewrite the classic attention mechanism in the non-vectorized form, which will help us describe the idea behind Latte.
Quick recap
One of the most common ways of writing a standard attention layer is using the matrix form:
Nonetheless, bearing in mind that standard attention is based on pairwise interactions between elements of a sequence, the formula can be written more intuitively without any vectorization. Defining a sequence of tokens
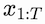from which we obtain the queries
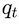keys
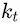and values
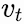we explain standard attention in Figure 1. Mathematically, one can write the above for the new
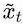vector:
and
Hence, the new representation of
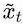is a combination of all elements, weighted by their similarity with the current token
.
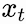To make the connection with the matrix form, we observe that
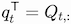and
.
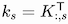Notice that we can think of
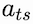as the probability of occurrence for a token at position
.
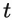This observation will help us understand our latent approach. Here we defined bidirectional standard attention, but for the causal case, we would sum up to index
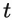instead of the entire sequence length
.
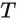This ensures that the new representation does not incorporate tokens in the future which are not available at test time.
Bidirectional Latte
As previously stated, the bottleneck of standard attention is computing weights
.
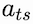We mitigate this by introducing learnable latent tokens that are compared to each element of the sequence. Since the number of latent tokens is fixed, the computation cost becomes linear in the sequence length. Intuitively, we can think
of the latent variables as concepts like colors or shapes to which we compare the input. Then our method creates a new representation using all the sequence tokens and their similarity to the learned high-level concepts. In Figure 2, we
show the difference between bidirectional Latte and bidirectional standard attention methods.
The approach has similarities with sparse attention methods such as BigBird, which only compute attention between a set of learnable global tokens and all the sequence elements. However, the main difference is that the sparse methods are weighted sums of the global tokens, while in our approach we consider the entire sequence. Specifically, we define a different parametrization of full attention using latent variables, instead of only performing attention between the latents and the sequence elements.
Defining our previous observation that attention has a probabilistic interpretation, we can re-parameterize
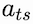with a weighted sum based on
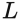learnable latent variables:
In the above, we assumed independence between
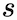and
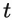give
.
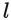Intuitively, we compute the similarity between a high-level concept and each element, then we re-weight it based on the similarity between our current token and the high-level concepts. These concepts are our latent variables, which we
learn end-to-end in tasks like classification or language modeling. Hence, they might not necessarily be interpretable. To calculate the probabilities above, we can reuse the attention matrices
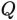and
,
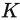giving us the new vector representation of each token:
Note that
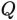and
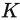have different sizes than the queries and keys in the standard attention. Figure 3 describes in detail how we obtain these matrices.
Our formulation results in
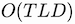time and
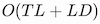memory complexity, compared to the
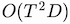of the standard bidirectional approach. We defined
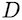to be the vector dimension. The approach is not entirely new. Other works have decomposed attention in the same fashion for the bidirectional case. However, our probabilistic framework easily allows us to extend our model to the causal
case.
Causal Latte
In the previous sections, we described the bidirectional case, but for problems like language generation, we need a causal mechanism. The change can be trivially seen by looking at the formula for
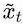and only sum up to index
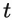instead of the entire sequence. This means that we have a cumulative sum and we cannot simply apply the softmax function over
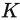Instead, we need an approach which updates sequentially the normalisation factor and the weight given by
.
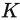Defining
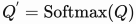and
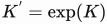we can write:
The formulation above can be vectorized. However, a sequential implementation has the benefit of constant time complexity for the next token prediction task. Hence, predicting
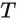tokens requires
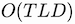time and
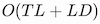memory.
Relative embeddings
Relative embeddings generalize better to unseen sequence length when compared to additive positional embeddings. However, in their standard form, they do not make sense to be used for latent tokens. We therefore introduce VAPOR (value embedded positional rotations) which computes the relative distance between tokens, but without affecting the attention weights:
Results
Runtime Efficiency
We developed a method with linear time and memory complexity in the sequence length. One drawback is that the causal version needs to be implemented sequentially to decrease memory usage and have constant time inference. If the sequence length is small, this can be slower than a vectorized version of standard attention on GPUs. To see the benefits of Latte, we perform an analysis of runtime performance in Figure 4.
From the above, we can see that the bidirectional case is faster than the standard attention even when the sequence length is small. However, the sequential causal model has a better runtime performance than causal attention only for sequences longer than 3,000 tokens. In terms of memory, Latte is more efficient even when the sequence has a smaller length. The results are dependent on the number of latent variables which give a tradeoff between runtime efficiency and the complexity of a model.
Long Range Arena
Long Range Arena is a synthetic benchmark which tests the ability of models to capture long-range dependencies on sequences of 2,000 to 16,000 tokens. All the tasks in the benchmark treat the input as a sequence of tokens and are formulated as classification problems. Consequently, the performance of the model is measured with accuracy, where a higher score means a better model.
We implement the tasks with a bidirectional Latte model using 40 latents and show that we outperform the standard attention. The low number of latents results in a model which is faster than the standard attention, while still having better performance. We also compare Bidirectional Latte to other efficient Transformers and obtain comparable results, with the benefit that our method could easily be applied in both causal and bidirectional cases.
Language generation
For language modeling, we train a Causal Latte model on the next token prediction task. The datasets used are Wiki103, OpenWebText, and Enwik8. We tokenize the first two with a byte pair encoding tokenizer, while for the latter we used a character tokenizer. The sequence lengths are 1,024 and 2,048 for the two tokenization types. Two common metrics that we also use to measure the success of this task are perplexity (PPL) and bits-per-character (BPC). PPL is the exponential of the negative log-likelihood, meaning that a lower score indicates a better model. Similarly, BPC is the negative log-likelihood transformed in based two such that it indicates the number of bits used to represent a character. Again, a lower score means a better model.
We set the number of latent variables
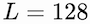such that the model is faster than the standard causal attention while obtaining comparable results, as reported in Table 2.
On token-level language modeling tasks, Latte combined with VAPOR obtains scores close to the standard attention. This is shown by experiments on Wiki103 and OpenWebText datasets. We also benchmark against Transformer-XL, a recursive model built for long sequences, and we get better results for a comparable number of parameters. While these results are promising considering the runtime gains, our model has some disadvantages on character-level data sets like Enwik8. For this setting, patterns are more difficult to observe and elementwise interaction between characters might be required to increase performance. Nonetheless, the results show a tradeoff between computational complexity and model capacity.
Final thoughts
Inspired by the fact that language can be decomposed into higher-level concepts, we developed a simple framework for bidirectional and causal cases that acts as a replacement for standard attention. Following the probabilistic interpretation, our model is easy to implement and has a fast and memory-effective runtime while it achieves better or comparable performance on classification and language generation tasks. Another benefit of our approach is that the next token prediction runs in constant time, resulting in a fast model during generation. Latte is a flexible model, which we would also like to apply in multimodal tasks like visual question answering. Check out our code for more details!
